Decibels are a way to compare numbers that are vastly different from each other in a way that resembles our experiences. Every 3 dB means a doubling, and every 10 dB means a factor of ten! This means 6 dB is four times greater, and 20 is a hundred times more energy. Do you want to nerd out? Here’s your chance, read on:
A decibel is a way to describe level differences. We established with listening tests that the threshold of human hearing is 20 µPa. That is a measure of pressure. 20 µPa = 2.0 * 10-5 Pa. Pa stands for Pascal, what’s in a name, and that is a pressure of 1 Newton per square meter. Suffice it to say that it is very little. But that is not silence! It is silence to most humans.
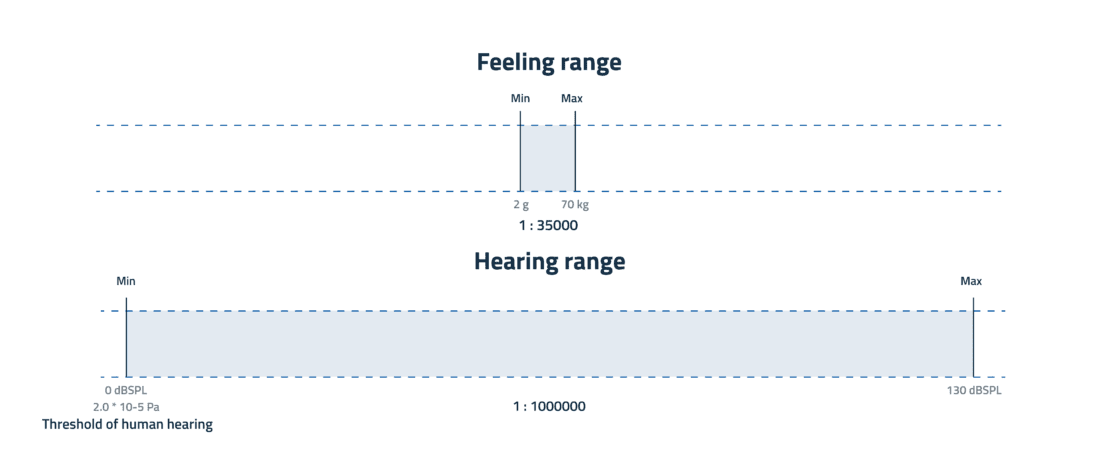
We decided to call that 0 dBSPL. Now here is a bit of math: a decibel is one tenth of a bell (named after Alexander Graham Bell).
100=1, so 0 dB
10 dBSPL = 1 bel. 101 = 10
Let’s condense this:

With a calculator you can get an exact number for every value in between. The takeaway here is that decibels are logarithmic and that is because our ears perceive the world logarithmically.
Note: These are values pertaining to power, both as in acoustic power and electric power. Because of ohms law these values are calculated differently for voltage and sound pressure.
The loudest sounds we can hear are around 130 dBSPL, that is in sound pressure level over 3 million time more. Our ear have a range between the softest and loudest sound of over one million in sound pressure. This is the reason why we need decibels.
Now the cool part. Whatever you are working with. A sound file, a microphone, an amplifier or a loudspeaker, a dB is a dB. So speaking twice as loud (in energy), or moving the gain up 3 dB, or the master fader. Increasing the input, gain, or output lever 3 dB will result in 3 dB more from your speaker. That makes decibels the preferred reference for audio engineers.

So a decibel is a factor. But a factor only has a real value if you know what the reference is. That is why you have different suffixes for dB:
dBSPL; reference is 2.0 * 10-5Pa, or the threshold of hearing
dBV; reference is 1 Volt, 0 dBV is 1 volt
dBm; reference is 1 mW (milliwatt), used in wireless signals
dBu; reference is 0,775 Volt*
dBFS; used in digital audio, reference is the maximum value. dBFS are always numbers below 0.
*Wait, what? Why is 0 dBu equal to 0.775 V? dBu is used in audio systems. The old reference for microphones is an impedance of 600 ohms. And 0 dBu across 600 will result in a power drawn of 1 mW! So 0 dBu across a resistor of 600 ohms in 0 dBm.
No for the downside. Because of the way our hearing works, with these giant differences in values, we need decibels. But using them sometime means that we do not see what a big number these represent. Some microphones have a nominal output of – 60 dBV. (See what we did there? Decibel can have negative values. – 60 dBV = 1 mV). That means that to achieve low noise figures, electronics have to have noise in the microvolts range or less. Amplifiers routinely have gain of 37 dB, so anything you feed to the amplifier comes out 37 dB louder (1 V in becomes about 70 V). This means that to achieve the 96 dB signal to noise ratio of Iris, you need clean, well-designed electronics.
